Introduction to Spatial Coordinate Systems: Flat Maps for a Round Planet

SQL Server Technical Article
Writers: Isaac Kunen
Project Editor: Diana Steinmetz
Published: July 2008
Summary: This paper is an introduction to Earth-oriented coordinate systems, projections, models, and mapping. While not specific to any technology, this information provides valuable background for those who will use spatial data in SQL Server.
Introduction: Teaching the Controversy
Contrary to popular opinion, Columbus did not prove that the Earth is round.[i] Pythagoras, Plato, and Aristotle claimed a round Earth based on philosophic and observational grounds. More impressively, Eratosthenes measured the Earth’s circumference around 240 B.C., a measurement which comes amazingly close to modern values—within 17 percent when taking pessimistic conversions into account and perhaps 2 percent if we’re more generous.
While there have always been—and likely will continue to be—people who steadfastly maintain that the Earth is flat, this is clearly an eccentric position. And yet, the most common representations of the Earth are flat maps. Thousands of years of effort have been put into flat representations of the Earth, and many of the techniques used are highly sophisticated and still quite valuable today.
The object of this short discussion is to explore this apparent contradiction and provide an introduction to both flat and round representations of the Earth, their uses, and their pitfalls, as well as to briefly discuss how modern developments continuously affect the way we work with the geospatial data. This is far from a comprehensive survey—entire books are devoted to these subjects—but we hope that this paper serves as a useful introduction to a surprisingly complex subject.
Flat for a Purpose
If we all agree that the world is round, why would anyone willfully flatten it?
To answer, let’s first revisit models. We use a model as a proxy for the thing it represents in order to simplify our reasoning about it. For example, if we want to measure the distance between New York and Paris, we can set out to measure the distance manually. A simple way to do this is by stretching a string between the two cities, but there are obvious practicalities that need to be overcome: Can we find a string long enough? How do we get the string across the Atlantic? Will the string stretch when it gets wet?
If we have a model of the system, the problem becomes a bit simpler. We can use a string to measure the distance on a globe, for instance, and then multiply this by the correct scale factor to obtain a distance on the Earth. The distance may not be perfectly accurate, but if the globe is large enough we should get a reasonable approximation. We also don’t need to worry about getting our string wet.
To be useful, a model must be a reasonable approximation of its subject, but it must also be easy to use: it must be both accurate and convenient. These two criteria are often at odds, but it is in convenience that we find the rationale for flattening the Earth.
Taking the mental step back into the time before the modern computer, we can consider the various options available to someone building a physical model of the Earth. As before, we could use a globe, but while this may be useful to envision the whole Earth, to achieve the detail needed for most real calculations, a truly gargantuan globe would be required. Instead of a whole globe, we can build a portion of a curved shell to more accurately represent some area of interest. While examples of these models can be found in museums, they are difficult both to fabricate and to transport.
Much more convenient are paper maps. They are easy to mass produce—at least since Gutenberg—easy to fold (or roll) and carry, and easy to use. Since the paper is flat, and the Earth is not, the data must be projected to the plane before it can be described on a paper map. As we will see, there are many ways to project, but they all distort the Earth, and this distortion degrades accuracy.
To illustrate the problem, let’s look at the very common Mercator projection (Figure 1). Although Alaska is a large state—more than twice the size of Texas, its nearest competition—it is hardly as large as it appears. Greenland presents a more extreme example: while in this projection it appears to be about the same size as Africa, it is in fact about fourteen times smaller. (Africa weighs in at a mighty 30 million square kilometers, easily trouncing Greenland’s 2.2 million.)
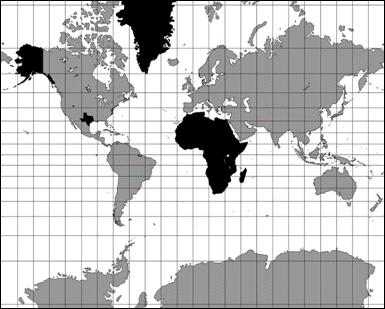
Figure 1: (Nearly) Whole-Earth Mercator projection
Given the scale of these distortions, you might wonder how a flat map could ever be a reasonable model. If, for example, we want to calculate the distance between Sydney and Beirut, we cannot simply look at the scale, measure the distance, and compute anything resembling an accurate value. Perhaps a map like this presents a reasonable way to view the Earth, but it seems to stretch the truth too much to be of value for most real computations.[ii]
Is Mercator a particularly poor projection? Unfortunately, no: any whole-Earth projection has serious distortions. One can correct for area, for example, but only by sacrificing some other measure. There are a great number of projections in use, but the solution to our problem lies not necessarily in abandoning the Mercator projection—it is, in fact, quite widely used—but rather in restricting the area in which it is used.
The Mercator projection is an example of a cylindrical projection: it takes each point on the Earth to a point on a cylinder, which is then unfurled and laid flat (Figure 2).[iii] If we examine a region near the circle where the cylinder touches the Earth—the equator in the most familiar construction—we find that the distortion is quite small. So, if we can content ourselves with a small distance from the equator, we can achieve quite accurate results with a Mercator projection.
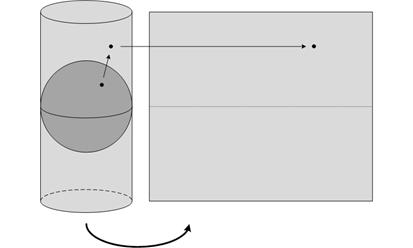
Figure 2: Constructing a Mercator projection [iv]
Not to slight Ecuadorians and Gabonese, but a map that is only accurate near the equator is of limited use for those of us in less tropical locales. Even we have hope in Mercator, however. While the usual Mercator projection uses a cylinder tangent to the Earth at the equator, there is no reason in principle to do so. A transverse Mercator projection, in contrast, uses a cylinder that is rotated 90 degrees and is tangent at a meridian (Figure 3a). A transverse Mercator is therefore accurate near that meridian, regardless of latitude. An oblique Mercator extends this further, by using a cylinder with any orientation (Figure 3b).
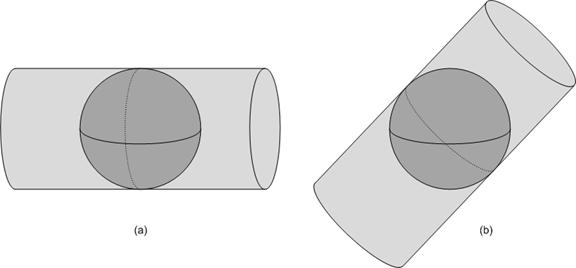
Figure 3: Transverse and oblique Mercator projections
Although Mercator projections are quite common, they are by no means the only projections commonly used. Of the many that have been devised—hundreds, for sure—we mention only one more here: the Lambert conformal conic. A Lambert conformal conic projection is similar to a Mercator projection, but it maps to a cone instead of to a cylinder (Figure 4). Unlike a Mercator projection, which is accurate in a band that follows a great circle, a Lambert conformal conic projection is accurate in a band around a small circle.[v] Figure 5 shows the difference between these projections.
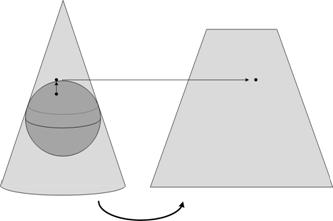
Figure 4: Constructing a Lambert conformal conic projection [vi]
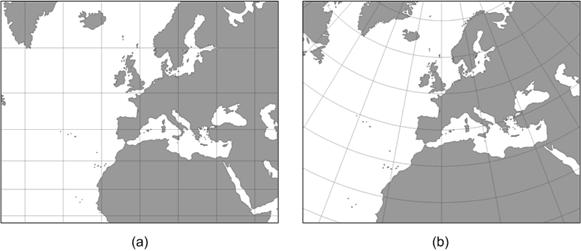
Figure 5: Mercator and Lambert conformal conic projections of Europe
By choosing the correct projection, and by restricting the area of the projections, we can create flat maps of a small area that are quite accurate. The obvious drawback to this is that we must operate in a restricted area. To operate over larger regions, we must make use of more than one projection, and therefore more than one map.
Models and Display
As we have seen, flat maps are distorted representations of the underlying data, and these distortions affect the accuracy of the calculations we perform when using the map. These problems can be kept to a minimum if we restrict the area in which we operate, and this has allowed people to make very effective use of flat maps. Let’s step back and consider our workflow.
We start with some objects on the Earth, and we project these to a plane using one of the many projections available to us. We then have our model—a paper map—which we can use to perform a calculation. For example, we could calculate the distance between two cities by measuring the distance between them on the map and multiplying by the appropriate scale factor. Displaying this model is trivial: the map is our vehicle for display. This workflow is described visually in Figure 6.
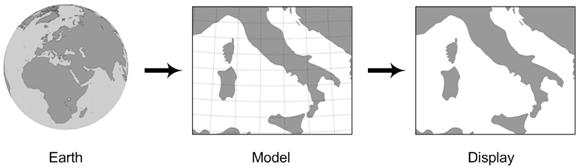
Figure 6: A workflow with a flat model
A modern computer allows for a very different workflow. Instead of using a flat model, we can build a spherical model of the Earth. Since the Earth is approximately a sphere, this model can represent the entire planet with very little distortion. We can now compute the distance between our two cities by using a spherical distance formula.
Because our displays are also two-dimensional flat surfaces, we still must project our data to the plane if we want to view it—but this projection happens after we perform any calculations. That is, this projection is for the convenience of the viewer, and its accuracy does not affect the accuracy of our calculations. This workflow is shown in Figure 7.
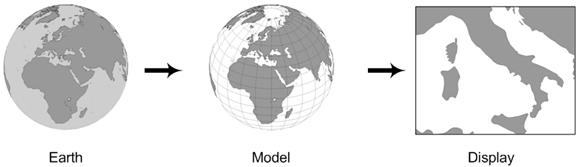
Figure 7: A workflow with a round model
Keep in mind that in principle none of this depends on computers: the math behind it is no more sophisticated than what is needed to create a flat map projection. What computers do is make this new workflow practical. Flat maps have a number of advantages: the more difficult mathematics are front-loaded into the construction of the model so the model is easier to use, and a flat model can be printed and easily transported. With modern computers, these advantages are less significant.
As long as there is a need for paper maps, we will still have uses for flat-Earth models, and as long as we must display maps on flat displays we will still need to ultimately project data to the plane. However, because mapping is increasingly done by computer, the round-Earth model appears ascendant.
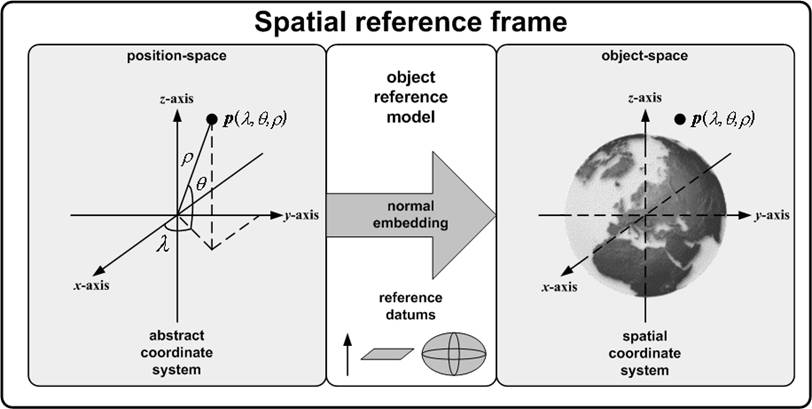
Coordinates
The way we express objects and perform calculations are quite different in flat- and round-Earth models. Both models have their uses, but these differences make interoperating between the two challenging.
First we will look at geographic coordinate systems assuming a spherical model of the Earth. We will revisit this assumption later, but for the moment it is a reasonable simplification.
Latitude and longitude are angular measures: latitude tells us the angle to which a point is elevated above the plane of the equator, as measured from the center of the Earth; longitude tells us how far east or west of the prime meridian a point is (Figure 8). Note that while the equator is naturally defined by the Earth’s rotation, the prime meridian is arbitrary, so we must agree on a prime meridian before we can interpret the coordinates we are given.
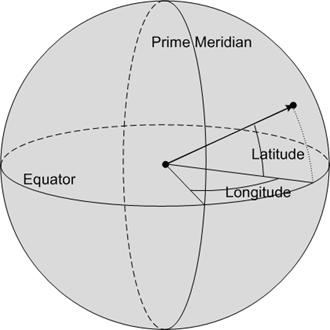
Figure 8: Measuring latitude and longitude
Taken together, the latitude and longitude do not uniquely define a point; they define a ray from the center of the Earth. Unless otherwise specified, we generally take this to refer to a point on the surface of the Earth, eliminating any ambiguity.
The landscape is a little different in the projected flat-Earth, or planar case. On the plane we do not make use of angular coordinates, rather we use a linear measure. A projected coordinate system will naturally have a center from which measurements can originate, and coordinates are specified by their linear distance east and north of that point; these measurements are called eastings and northings, and are given in some linear measure, typically meters or feet. Generally, these coordinates are shifted by adding some amount to each coordinate so that they are strictly positive numbers; the resulting values are sometimes called false eastings and false northings (Figure 9). (These are often still referred to as simply eastings and northings colloquially.)
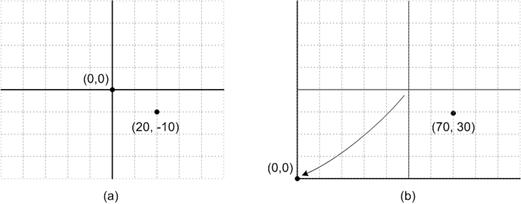
Figure 9: Eastings and northings (a) and false eastings and false northings (b) for the same point
When printed, a projected map can be combined with a scale that gives a conversion factor from the map to the Earth. With this, we can use a ruler to measure the distance between two points on a map and convert these into a distance value on the Earth. As we’ve discussed, there will be some distortion in the map, so these values will not be perfectly accurate, but generally this error is kept low.
While it is intuitive to equate latitude with northings and longitude with eastings, this association is problematic. For example, although the coordinate space of a flat map near the equator may line up well with a latitude-longitude grid, a flat map over the pole clearly does not (Figure 10). Because of this, the terms eastings and northings are usually dropped for polar maps. Keep in mind that while this example is somewhat extreme, such deviations occur at any latitude other than zero.
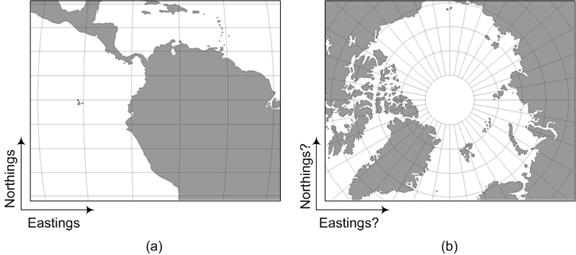
Figure 10: Eastings and northings make less sense at the Poles
We should also keep in mind that latitude and longitude are not linear measures, and a planar calculation of distance using them makes little sense. Although lines of latitude, or parallels, are evenly spaced, and could be converted to a linear distance, the distance between lines of longitude, or meridians, varies with latitude. If we apply the formula for Euclidean distance between two points expressed in latitudes and longitudes, we end up with a value that makes very little sense.
For example, consider Figure 11(a). If we use latitude and longitude coordinates and compute the distance between Palermo and Ancona, we end up with a meaningless value of about 5.502.
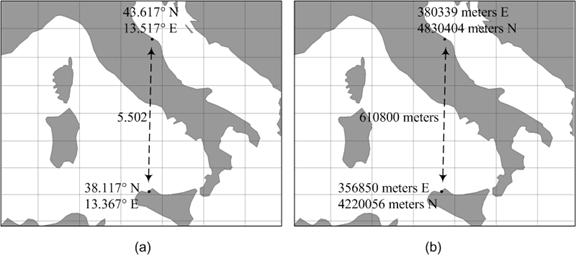
Figure 11: The Euclidean distance only works for planar coordinates
Figure 11(b) shows the same points as Figure 11(a), but represents them in a planar coordinate system using meters east and north of a control point at the equator.[vii] If we compute the Euclidean distance using these values, we find that the distance is 610,800, but we now know the unit to be meters. We can also compute this distance using a round Earth model and find the value to be 610,914. There is some error in our planar calculation—about .02%—but the value is remarkably close. Planar models are not perfect, but can provide very accurate results when used correctly.
Common Coordinate Systems
If we have a large area to cover, and if wish to use paper maps to perform accurate calculations—rather than simply to look nice hanging on the wall—we must divide our area of interest into smaller regions and use a different projected coordinate system for each.
In the United States, the most common such set of coordinate systems is the State Plane system (Figure 12). This system decomposes each state into one or more pieces and defines a separate coordinate system, each with a different underlying projection, on each piece. The projections used are chosen from the ones we have already discussed based on the shape of each region: tall, narrow regions use a transverse Mercator projection; wide, short regions use a Lambert conformal conic projection; and the Alaska panhandle (not shown) uses an oblique Mercator projection.
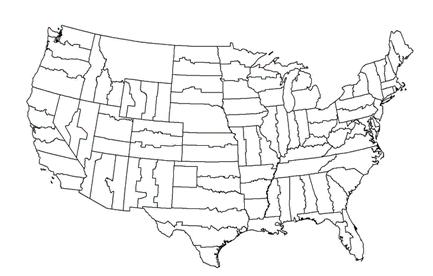
Figure 12: The State Plane system (continental United States only)
By decomposing the United States in this way, coordinate systems can be defined so that the error is relatively small: by design, distances are off by no more than one part in 10,000. That is, if we were to measure a distance of 10 miles on a state plane map, we would be off by no more than about five feet. This level of accuracy makes these maps attractive to state and local governments, who use them for laying out roads, properties, and the like.
Other countries similarly define such coordinate systems, although smaller countries may use a single system throughout. There are also global systems that can be used independent of a particular country, such as the Universal Transverse Mercator (UTM) system. As its name implies, UTM is a set of coordinate systems based on transverse Mercator projections, and covers the entire Earth between 80°S and 84°N latitude (Figure 13).
The UTM system comprises 60 transverse Mercator projections, one for each 6° slice of the globe. The coordinates are shifted in each slice so that the point on the equator in the center of each zone is assigned the false easting of 500,000 meters. This same point is given the false northing of 0 when working with coordinates in the northern hemisphere, and the false northing of 10,000,000 meters when working in the southern hemisphere. This guarantees that any point in the zone can be described with entirely positive coordinates. The planar coordinates in Figure 11 are given in UTM zone 33. (The geographic coordinates are in WGS-84, which we will come to.)
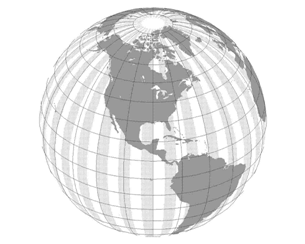
Figure 13: The UTM zones (simplified)
Decomposing a large region and projecting each piece separately solves our main problem—we can produce accurate maps, and use them to perform geographic calculations—but it introduces another issue: what to do between regions. This issue injects a great deal of complexity into any problem where it is encountered, and we will not address it here. Round-Earth models avoid this problem.
A Better Earth Model
So far, we have made the simplifying assumption that the Earth is a perfect sphere. Looking at the many bumps and hills we see, this is clearly not the case. Although a topographic map roughly describes these, clearly we cannot accurately model every minor bump: not only are they too numerous, they change too rapidly. In this section, we take a look at a few approximations that can be used.
The first step of approximation is the geoid, which is a theoretical construct defined as a surface of equal gravitational potential. If we ignore other forces, a body of water will flow so that its surface has equal gravitational potential. This means that on the ocean, the geoid closely matches mean sea level. Elsewhere, the surface of the Earth may rise (or fall) above (or below) the geoid. Although a large mass like a mountain causes the geoid to deviate somewhat, the geoid often lies far from the surface of the Earth (Figure 14).
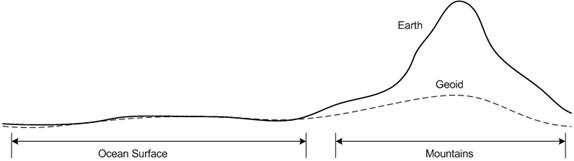
Figure 14: Earth versus the geoid
Although the geoid can deviate greatly from the surface of the Earth, it is a valuable physical construct. Because it is an equipotential surface, a plumb-bob at the geoid always hangs perpendicular to the geoid. That is, at the geoid, “up” is always perpendicular to the surface.
The geoid, however, is an irregular structure that has no concise mathematical description. From careful measurements, a close approximation can be described by using spherical harmonics. [viii] Working with the resulting model can be very complex. Instead, for most applications, an ellipsoidal model of the Earth is more than sufficient. A best-fit ellipsoid for the Earth is about .3% shorter than it is wide, and differs from the geoid vertically by about 100 meters at worst (Figure 15). Despite its lumps, the geoid is almost ellipsoidal.

Figure 15: The geoid versus the ellipsoid
One more step in our approximation brings us to the sphere. Whereas the ellipsoid is quite a close fit to the geoid, the sphere deviates significantly: the equatorial radius of the Earth is about 21 kilometers longer than the polar radius, so a best-fit sphere will separate from the geoid by about 10.5 kilometers.
Because of its simplicity and close fit, the ellipsoid seems like a reasonable level of approximation at which to work, but this choice does introduce some unexpected complexities. For example, the definition of latitude is no longer completely clear. One value we could choose is called the geocentric latitude. This is the latitude as we defined it previously: the angle between a ray from the center of the ellipsoid to the point and the plane of the equator.
Generally, a different measure is used: the geodetic latitude. This measure is the angle of the vector perpendicular to the ellipsoid at the point of interest. For a sphere, this measure exactly matches the geocentric latitude, but, as illustrated in Figure 16, it will not match on a general ellipsoid. The illustration is for a very flattened ellipsoid; for an ellipsoid modeling the Earth, this deviation is no more than about 1/5 of a degree, but even this translates into a worst-case difference of more than 20 km on the surface of the Earth.
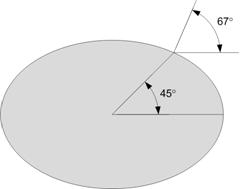
Figure 16: Geocentric versus geodetic latitude (an extreme example)
Other complexities are introduced by an ellipsoidal model (such as how to define the path between two points) but these can be overcome. The mathematics for dealing with an ellipsoid are somewhat more complicated than those for the plane or sphere, but are easily handled by a modern computer.
Ellipsoids, Datums, and Projections
When we give the coordinates of a location, we should be careful that we are clear in our meaning. The eastings and northings of a particular point clearly depend on the projection employed, but even geographic coordinates are not unique.
An ellipsoidal model can very accurately represent the Earth, but it does not do so exactly. This has led people to devise various ellipsoidal models that conform more closely to their particular areas of interest. Also, we continue to refine our models as our ability to accurately measure the Earth increases. Taken together, these factors have given rise to a large number of different ellipsoidal models, each with an associated coordinate system.
To define a geographic coordinate system, we first need an ellipsoid definition. Ellipsiods are defined by the lengths of their two axes: the semiminor, which runs halfway between the poles; and the semimajor, which crosses half way from one side of the equator to the other.[ix] Any ellipsoid used to approximate the Earth must, of course, approximate the Earth, and so the ellipsoids used are all very similar. They are, however, not exactly the same.
For example, the WGS-84 (World Geodetic System of 1984) ellipsoid, used by the Global Positioning System, has a semimajor radius of 6,378,137 meters and a semiminor radius of 6,356,752.314 meters. An older, but commonly used ellipsoid is the Clarke 1866 ellipsoid, with a semimajor radius of 6,378,206.4 meters and a semiminor radius of 6,356,583.8 meters. While these differences may seem small, they must be taken into account if we wish to be precise.
After we agree on an ellipsoid, we still must decide how that ellipsoid is affixed to the Earth before we have a usable geographic coordinate system. How exactly this is done is called the datum of a coordinate system.
To see how this works, first consider Figure 17(a). Although most coordinate systems used for the entire Earth place the center of the ellipsoid at (or near) the center of the Earth, a better fit to the actual area of interest may be achieved by shifting this center. The figure represents a caricature of a planet with greatly magnified irregularities. The shifted (dashed) ellipsoid is a better match to the large northern plateau than the same ellipsoid with its center at the center of the planet.
Figure 17(b) shows the same ellipsoid with two different prime meridians. Unlike the equator, choice of the prime meridian is arbitrary and may be made to place longitudes in a convenient range or for political reasons. (Perhaps not everyone wants their prime meridian to run through Greenwich.)
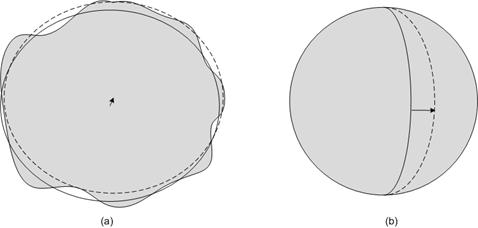
Figure 17: Shifting datum centers and prime meridians
Although some models are relatively close, in order for coordinates to be truly compatible, they must be represented in the same model. Computations done on mixed data produce inherently flawed results.
Be aware that there is often some overloading of terms when discussing coordinate systems. The WGS-84 coordinate system is defined by the WGS-84 ellipsoid and the WGS-84 datum, but these pieces may be reused elsewhere. For example, the Korean 1995 coordinate system makes use of the WGS-84 ellipsoid along with the Korean datum of 1995.
Planar coordinate systems have the complexity of their projection, but this is in addition to everything just discussed, since the projection will be from some ellipsoidal Earth model to the plane. To accurately map a point on the Earth when using a planar system, we must know the ellipsoid, datum, and projection being used.
Conclusion
Maps are deceivingly simple tools, and cartography a surprisingly complex discipline. While the most trouble many of us will have with a map is figuring out how to fold it, this simplicity belies great sophistication that has been developed over the years. While a short paper cannot fully explore the nuances of this field, we hope that this one provides a useful introduction to the theory and practice of modeling the Earth.
Did this paper help you? Please give us your feedback. Tell us on a scale of 1 (poor) to 5 (excellent), how would you rate this paper and why have you given it this rating? For example:
- Are you rating it high due to having good examples, excellent screenshots, clear writing, or another reason?
- Are you rating it low due to poor examples, fuzzy screenshots, unclear writing?
This feedback will help us improve the quality of white papers we release. Send feedback.
End Notes
[i] Columbus was an iconoclast, but rather than bringing reason to an establishment entrenched in a flat-Earth worldview, he argued, based on wildly incorrect reasoning and information, that the trip to India would be much shorter than experts believed, and therefore reachable by ship. As is often the case, the experts were correct, but Columbus, tripped up by an unexpected continent in his way, got the glory.
[ii] The Mercator projection does have the property that courses of constant bearing—rhumb lines—are straight lines in the projection. This makes Mercator useful indeed when plotting a ship’s course.
[iii] There are many ways to map to the plane, even if we stick with a cylindrical mapping, but the specifics are beyond the scope of this discussion.
[iv] A slightly smaller cylinder is often used, resulting in an intersection with the sphere at two circles. This produces a projection that has no distortion at those two lines, is stretched outside the two lines, and is compressed slightly between them. This procedure extends the region in which the projection can be used without significant distortion.
[v] A great circle is a circle that is formed by the intersection of the Earth with a plane that passes through the center of the Earth. A small circle is formed by the intersection of the Earth with a plane that does not pass through the center of the Earth.
[vi] As with the Mercator projection, a slightly smaller cone is often used, resulting in two circles of zero distortion.
[vii] The geographic coordinates used here are in a system called WGS-84, and the planar coordinates are in UTM Zone 32. We’ll look at these in more depth later.
[viii] These measurements are not trivial to carry out and are the subject of active scientific work. At the time of this writing, the Gravity Recovery and Climate Experiment (GRACE) is using two satellites to accurately map the geoid and measure changes over time.
[ix] An ellipsoid can have three dissimilar axes, one in each of the three dimensions. All ellipsoids used to model the Earth have two of them equal, and so the equator is a perfect circle.